Кривые Безье
Исходные данные: набор кривых Безье (шаблонов), произвольный набор координат точек образующих фигуру ("проверяемую").
Задача: определить степень похожести проверяемой фигуры заданной набором точек и шаблона заданного кривой Безье.
Для начала рассмотрим очень упрощенно, и лишь для одного куска кривой Безье. Например для кривой Безье, заданной тремя контрольными точками A, B, C:

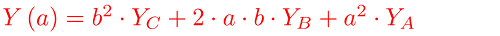


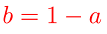
XA, YA, ZA, XB, YB, ZB, XC, YC,ZC - координаты x, y, z исходных узлов A, B, C соответственно.
Тогда, если подставлять вместо X(a), Y(a), Z(a) координаты точки из проверяемой фигуры, можно находить для каждого уравнения значение коэффициента а:



Берём только те а, которые положительны, тогда "точность" попадания точки в шаблон, можно будет определять по тому, как точно совпадают эти три значения. Например можно оценивать это в относительных единицах, используя среднюю квадратическую сумму "коэффициентов похожести":
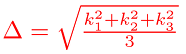
где "коэффициент похожести" определяется как:


 (FIXME: yx should be ay)
(FIXME: yx should be ay)
Чем ближе полученное значение Δ к 1, тем точнее попадание.
Или, для ускорения обсчетов, можно рассчитывать среднее арифметическое:

В итоге становится понятно, как определить степень попадания одной точки в область линии. А дальше идёт рутинная работа, вроде определения степени попадания каждой из точек, определения весового коэффициента для них (в простейшем случае — 1/N для каждой, однако при неравномерных расстояниях между точками такой подход уже не годится), и определение "общей" степени попадания набора точек в заданную кривую. При использовании шаблона сложенного из нескольких кривых Безье ситуация немного усложняется тем, что неизвестно с какого момента нужно сравнивать точки со следующей кривой.
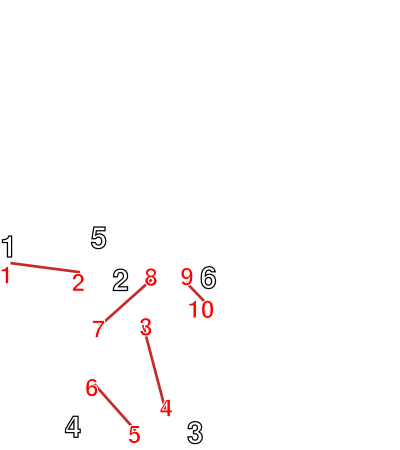
В качестве альтернативы, из набора точек можно генерировать новую кривую Безье и пытаться сравнивать её уравнения с уравнением исходной кривой. Самый первый "недостаток" этого метода в том, что точки должны быть упорядочены. Кроме того, либо узлов в этой кривой будет столько же сколько было точек, либо "отрезков" кривых Безье будет примерно столько же (каждый из отрезков лежит между двумя соседними точками), а это может быть в разы больше чем количество кривых шаблона. И равномерность расстояний между точками проверяемой фигуры тоже начинает влиять на результат. Существуют алгоритмы упрощения кривых Безье, благодаря которым можно уменьшить количество полученных кривых, а также уменьшить влияние равномерности расстояний между точками. Я оценил работу одного из таких алгоритмов на примере буквы греческого алфавита гамма:
Статьи в интернете для лучшего понимания, что такое кривые Безье: статья c Gamedev, статья Википедии, интересная статья о упрощении кривых Безье с www.rsdn.ru (archived)
Задача: определить степень похожести проверяемой фигуры заданной набором точек и шаблона заданного кривой Безье.
Для начала рассмотрим очень упрощенно, и лишь для одного куска кривой Безье. Например для кривой Безье, заданной тремя контрольными точками A, B, C:

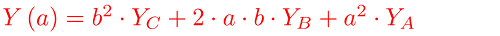


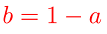
XA, YA, ZA, XB, YB, ZB, XC, YC,ZC - координаты x, y, z исходных узлов A, B, C соответственно.
Тогда, если подставлять вместо X(a), Y(a), Z(a) координаты точки из проверяемой фигуры, можно находить для каждого уравнения значение коэффициента а:



Берём только те а, которые положительны, тогда "точность" попадания точки в шаблон, можно будет определять по тому, как точно совпадают эти три значения. Например можно оценивать это в относительных единицах, используя среднюю квадратическую сумму "коэффициентов похожести":
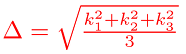
где "коэффициент похожести" определяется как:


 (FIXME: yx should be ay)
(FIXME: yx should be ay)Или, для ускорения обсчетов, можно рассчитывать среднее арифметическое:

В итоге становится понятно, как определить степень попадания одной точки в область линии. А дальше идёт рутинная работа, вроде определения степени попадания каждой из точек, определения весового коэффициента для них (в простейшем случае — 1/N для каждой, однако при неравномерных расстояниях между точками такой подход уже не годится), и определение "общей" степени попадания набора точек в заданную кривую. При использовании шаблона сложенного из нескольких кривых Безье ситуация немного усложняется тем, что неизвестно с какого момента нужно сравнивать точки со следующей кривой.
В качестве альтернативы, из набора точек можно генерировать новую кривую Безье и пытаться сравнивать её уравнения с уравнением исходной кривой. Самый первый "недостаток" этого метода в том, что точки должны быть упорядочены. Кроме того, либо узлов в этой кривой будет столько же сколько было точек, либо "отрезков" кривых Безье будет примерно столько же (каждый из отрезков лежит между двумя соседними точками), а это может быть в разы больше чем количество кривых шаблона. И равномерность расстояний между точками проверяемой фигуры тоже начинает влиять на результат. Существуют алгоритмы упрощения кривых Безье, благодаря которым можно уменьшить количество полученных кривых, а также уменьшить влияние равномерности расстояний между точками. Я оценил работу одного из таких алгоритмов на примере буквы греческого алфавита гамма:
- Вручную мне удалось изобразить её с помощью кривых Безье используя 6 узлов (2 кривые).
- Используя "аппроксимацию на глаз" прямыми отрезками было получено 40-70 узлов, которые, после "сглаживания", алгоритм упрощения из Inkscape уменьшал до 10-17 (медиана около 12).
Поэтому, несмотря на первоначальную привлекательность сравнивать с помощью генерирования новых кривых Безье или невозможно, или требует каких-то дополнительных преобразований, до которых я не дошел. Итого: я нашел только один способ которым, при доработке, можно сравнивать шаблон из кривых Безье с дискретным набором координат. Потенциальные особенности такого подхода:
- Может быть реализован так, что не будет зависеть от порядка точек в проверяемой фигуре и от равномерности/неравномерности расстояний между ними. Однако в этом случае "весомость" каждой точки придется считать одинаковой, либо хотя бы порядок должен быть известен.
- Чувствителен к преобразованиям массива точек (сдвиг, поворот, масштабирование)
- Может игнорировать целостность проверяемой фигуры. Например: все имеющиеся точки могут точно попадать в кривую, однако при этом покрывают лишь малую её часть, или не покрывают важные характерные изгибы. Может быть решено с помощью анализа того как рассчитанные значения коэффициента a покрывают диапазон 0 .. 1
- Может быть слишком чувствительным к некоторым аномалиям проверяемой фигуры (неравномерные расстояния между точками, "шум" и т.п.)
- Данный метод может быть неудобен, если надо сравнивать поочередно со многими шаблонами.
Возможно самый "простой" подход будет более эффективным: кривая Безье рендерится в растровое изображение, а затем сравнивается с набором точек используя один из "стандартных" алгоритмов сравнения изображений.
Статьи в интернете для лучшего понимания, что такое кривые Безье: статья c Gamedev, статья Википедии, интересная статья о упрощении кривых Безье с www.rsdn.ru (archived)